Kompletne systemy funkcji logicznych – Implikacja i inhibicja

0 0

Kompletne systemy funkcji boolowskich – implikacja i inhibicja wszystko o funkcjach boolowskich , funkcje boolowskie :

Obsah článku:

Kompletne systemy funkcji logicznych – Implikacja i inhibicja

Implikacja

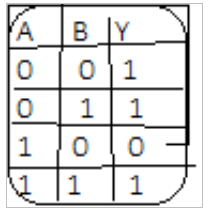
jest taką funkcją dwóch zmiennych A, B, Gdzie zmienna zależna Y przyjmuje wartość 0 tylko wtedy, gdy prawdą jest, że A przyjmuje wartość 1 i jednocześnie B przyjmuje wartość 0. W pozostałych przypadkach zmienna Y przyjmuje wartość 1. Aby utworzyć powyższe stwierdzenie używamy łącznika logicznego,, jeśli…., to

Notacja algebraiczna Y=A=>B

You might be interested in :

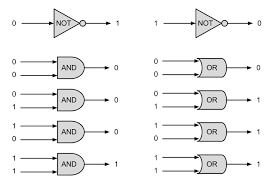
Kontaktowa implementacja operatorów logicznych

Tabela prawdy:

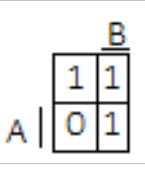
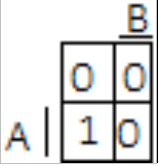
Mapa Karnaugha:

Inhibicja

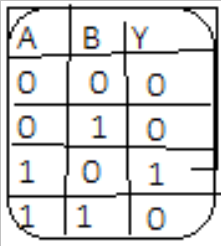
Jest to taka funkcja dwóch zmiennych A, B, w której zmienna zależna Y przyjmuje wartość 1 wtedy i tylko wtedy, gdy A przyjmuje wartość 1 i jednocześnie B przyjmuje wartość 0. W przeciwnym razie zmienna Y przyjmuje wartość 0. Aby utworzyć powyższe stwierdzenie używamy łącznika logicznego, jeśli…., to”

Notacja algebraiczna Y= A <= B